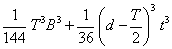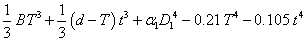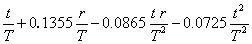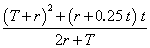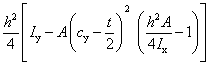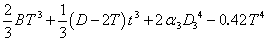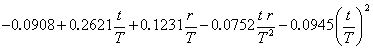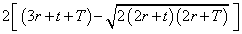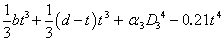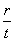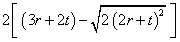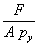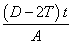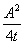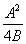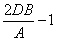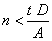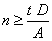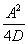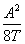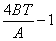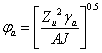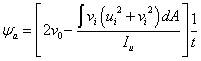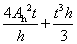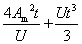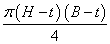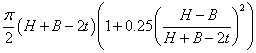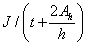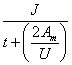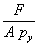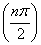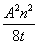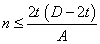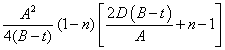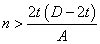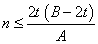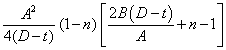3.1 General
All section properties have been accurately calculated and rounded to three significant figures. They have been calculated from the metric dimensions given in the appropriate standards (see Section 1.2). For angles, BS EN 10056-1 assumes that the toe radius equals half the root radius.
3.2 Sections other than hollow sections
3.2.1 Second moment of area (I)
The second moment of area of the section, often referred to as moment of inertia, has been calculated taking into account all tapers, radii and fillets of the sections.
3.2.2 Radius of gyration (r)
The radius of gyration is a parameter used in buckling calculation and is derived as follows:
r = [I / A]1/2
where:
| A |
is the cross‑sectional area. |
3.2.3 Elastic modulus (Z)
The elastic modulus is used to calculate the elastic moment capacity based on the design strength of the section or the stress at the extreme fibre of the section from a known moment. It is derived as follows:
Z = I / y
where:
| y |
is the distance to the extreme fibre of the section from the elastic neutral axis. |
The elastic moduli of the tee are calculated at the outer face of the flange and toe of the tee formed at the net section.
For parallel flange channels, the elastic modulus about the minor (y‑y) axis is given at the toe of the section, i.e.:
y = B – cy
where:
| B |
is the width of the section |
| cy |
is the distance from the back of the web to the centroidal axis. |
For angles, the elastic moduli about both axes are given at the toes of the section, i.e:
where:
| A |
is the leg length perpendicular to x‑x axis |
| B |
is the leg length perpendicular to y‑y axis |
| cx |
is the distance from the back of the angle to the centre of gravity, referred to as the x‑x axis |
| cy |
is the distance from the back of the angle to the centre of gravity, referred to as the y‑y axis. |
3.2.4 Buckling parameter (u) and torsional index (x)
The buckling parameter and torsional index used in buckling calculations are derived as follows:
(a) For bi‑symmetric flanged sections and flanged sections symmetrical about the minor axis only:
| u |
= [(4 Sx2 g / (A2 h2)]1/4 |
| x |
= 0.566 h [A/J]1/2 |
(b) For flanged sections symmetric about the major axis only:
| u |
= [(Iy Sx2 g / (A2 H)]1/4 |
| x |
= 1.132 [(A H) / (Iy J)]1/2 |
where:
| Sx |
is the plastic modulus about the major axis |
| γ |
= [1 – Iy/Ix] |
| Ix |
is the second moment of area about the major axis |
| Iy |
is the second moment of area about the minor axis |
| A |
is the cross‑sectional area |
| h |
is the distance between shear centres of flanges (for T sections, h is the distance between the shear centre of the flange and the toe of the web) |
| H |
is the warping constant |
| J |
is the torsion constant. |
3.2.5 Warping constant (H) and torsion constant (J)
(a) I and H sections
The warping constant and torsion constant for I and H sections are calculated using the formulae given in the SCI publication P057 Design of members subject to combined bending and torsion[12].
(b) Tee sections
For Tee sections cut from UB and UC sections, the warping constant (H) and torsion constant (J) have been derived as given below.
| H |
= 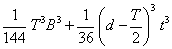 |
| J |
= 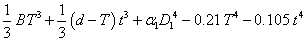 |
where:
| α1 |
= – 0.042 + 0.2204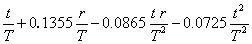 |
| D1 |
= 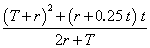 |
Note: These formulae do not apply to tee sections cut from joists which have tapered flanges. For such sections, details are given in SCI Publication P057[12].
(c) Parallel flange channels
For parallel flange channels, the warping constant (H) and torsion constant (J) are calculated as follows:
| H |
= 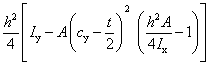 |
| J |
= 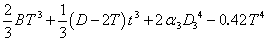 |
where:
| cy |
is the distance from the back of the web to the Centroidal axis |
| α3 |
= 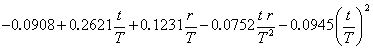 |
| D3 |
= 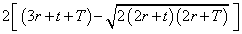 |
Note: The formula for the torsion constant (J) is applicable to parallel flange channels only and does not apply to tapered flange channels.
(d) Angles
For angles, the torsion constant (J) is calculated as follows:
J =
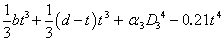
where:
| α3 |
= 0.0768 +0.0479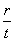 |
| D3 |
= 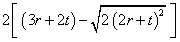 |
3.2.6 Plastic modulus (S)
The full plastic moduli about both principal axes are tabulated for all sections except angle sections. For angle sections, BS 5950-1: 2000 requires design using the elastic modulus.
The reduced plastic moduli under axial load are tabulated for both principal axes for all sections except asymmetric beams and angle sections. For angle sections, BS 5950-1: 2000 requires design using the elastic modulus.
When a section is loaded to full plasticity by a combination of bending and axial compression about the major axis, the plastic neutral axis shifts and may be located either in the web or the tension flange depending on the relative values of bending and axial compression. Formulae giving the reduced plastic modulus under combined loading have to be used, which use a parameter n as follows:
| n |
= 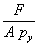 |
(This is shown in the member capacity tables as F/Pz) |
where:
| F |
is the factored axial load |
| A |
is the cross‑sectional area |
| py |
is the design strength of the steel. |
For each section, there is a "change" value of n. Formulae for reduced plastic modulus and the "change" value are given below.
(a) Universal beams, universal columns and bearing piles
If the value of n calculated is less than the change value, the plastic neutral axis is in the web and the formula for lower values of "n" must be used. If n is greater than the change value, the plastic neutral axis lies in the tension flange and the formula for higher values of n must be used. The same principles apply when the sections are loaded axially and bent about the minor axis, lower and higher values of n indicating that the plastic neutral axis lies inside or outside the web respectively.
Major axis bending:
| Reduced plastic modulus: |
Change value: |
| Srx |
= K1 – K2 n2 |
for |
n < 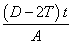 |
| Srx |
= K3 (1 – n) (K4 + n) |
for |
n ≥ 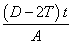 |
where:
Minor axis bending:
| Reduced plastic modulus: |
Change value: |
| Sry |
= K1 – K2 n2 |
for |
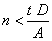 |
| Sry |
= K3 (1 – n) (K4 + n) |
for |
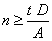 |
where:
(b) Parallel flange channels
Major axis bending:
If the value of n calculated is less than the change value, the plastic neutral axis is in the web and the formula for lower values of n must be used. If n is greater than the change value, the plastic neutral axis lies in the flange and the formula for higher values of n must be used.
| Reduced plastic modulus: |
Change value: |
| Srx |
= K1 – K2 n2 |
for |
n < 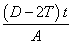 |
| Srx |
= K3 (1 – n) (K4 + n) |
for |
n ≥ 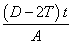 |
where:
Minor axis bending:
In calculating the reduced plastic modulus of a channel for axial force combined with bending about the minor axis, the axial force is considered as acting at the centroidal axis of the cross‑section whereas it is considered to be resisted at the plastic neutral axis. The value of the reduced plastic modulus takes account of the resulting moment due to eccentricity relative to the net centroidal axis.
The reduced plastic modulus of a parallel flange channels bending about the minor axis depends on whether the stresses induced by the axial force and applied moment are the same or of opposite kind towards the back of the channel. Where the stresses are of the same kind, an initial increase in axial force may cause a small initial rise of the “reduced” plastic modulus, due to the eccentricity of the axial force
For each section there is again a change value of n. For minor axis bending the position of the plastic neutral axis when there is no axial load may be either in the web or the flanges. When the value of n is less than the change value, the formula for lower values of n must be used. If n is greater than the change value, the formula for higher values of n must be used.
The formulae concerned are complex and are therefore not quoted here.
3.2.7 Equivalent slenderness coefficient (ϕa ) and monosymmetry index (ψa )
The equivalent slenderness coefficient (ϕa ) is tabulated for both equal and unequal angles. Two values of the equivalent slenderness coefficient are given for each unequal angle. The larger value is based on the major axis elastic modulus (Zu) to the toe of the short leg and the lower value is based on the major axis elastic modulus to the toe of the long leg.
The equivalent slenderness coefficient (ϕa ) is calculated as follows:
Definitions of all the individual terms are given in BS 5950-1[1], Clause B.2.9.
The monosymmetry index (ψa ) is only applicable for unequal angles and is calculated as follows:
Definitions of all the individual terms are given in BS 5950-1[1], Clause B.2.9.
3.3 Hollow sections
Section properties are given for both hot-finished and cold-formed hollow sections. The ranges of hot-finished and cold-formed sections covered are different. The section ranges listed are in line with sections that are readily available from the major section manufacturers. For the same overall dimensions and wall thickness, the section properties for hot-finished and cold-formed sections are different because the corner radii are different.
3.3.1 Common properties
For comment on second moment of area, radius of gyration and elastic modulus, see Section 3.2.1, 3.2.2 and 3.2.3.
For hot-finished square and rectangular hollow sections, the sectional properties have been calculated, using corner radii of 1.5t externally and 1.0t internally, as specified by BS EN 10210‑2[9].
For cold-formed square and rectangular hollow sections, the sectional properties have been calculated, using the external corner radii of 2t if t ≤ 6 mm, 2.5t if 6 mm < t ≤ 10 mm and 3t if t > 10 mm as specified by BS EN 10219-2[10]. The internal corner radii used is 1.0t if t ≤ 6 mm, 1.5t if 6 mm < t ≤ 10 mm and 2t if t > 10 mm, as specified by BS EN 10219-2[10].
3.3.2 Torsion constant (J)
For circular hollow sections:
J = 2I
For square and rectangular hollow sections:
J =
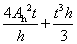
For elliptical hollow sections:
J =
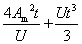
where:
| I |
is the second moment of area |
| t |
is the thickness of section |
| h |
is the mean perimeter = 2 [(B – t) + (D – t)] – 2 Rc (4 - π) |
| Ah |
is the area enclosed by mean perimeter of a square or rectangular hollow section and = (B – t) (D – t) – Rc2 (4 - π) |
| B |
is the breadth of section |
| D |
is the depth of section |
| Rc |
is the average of internal and external corner radii. |
| Am |
is the area enclosed by the mean perimeter of an elliptical hollow sections and = 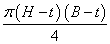 |
| U |
= 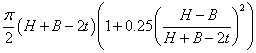 |
3.3.3 Torsion modulus constant (C)
For circular hollow sections
C = 2Z
For square and rectangular hollow sections
C =
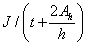
For elliptical hollow sections
C =
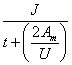
where:
| Z |
is the elastic modulus and J, t, , h, and U are as defined in Section 3.3.2. |
3.3.4 Plastic modulus of hollow sections (S)
The full plastic modulus (S) is given in the tables. When a member is subject to a combination of bending and axial load the plastic neutral axis shifts. Formulae giving the reduced plastic modulus under combined loading have to be used, which use the parameter n as defined below.
| n |
= 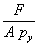 |
(This is shown in the member capacity tables as F/Pz) |
where:
| F |
is the factored axial load |
| A |
is the cross‑sectional area |
| py |
is the design strength of the steel. |
For square and rectangular hollow sections there is a "change" value of n. Formulae for reduced plastic modulus and "change" value are given below.
(a) Circular hollow sections
Sr =
S cos
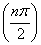
(b) Square and rectangular hollow sections
If the value of n calculated is less than the change value, the plastic neutral axis is in the webs and the formula for lower values of n must be used. If n is greater than the change value, the plastic neutral axis lies in the flange and the formula for higher values of n must be used.
Major axis bending:
| Reduced plastic modulus: |
Change value: |
| Srx |
= Sx - 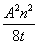 |
for |
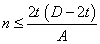 |
| Srx |
= 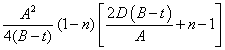 |
for |
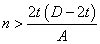 |
Minor axis bending:
| Reduced plastic modulus: |
Change value: |
| Sry |
= Sy - 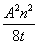 |
for |
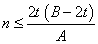 |
| Srx |
= 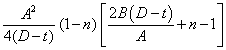 |
for |
 |
where:
| S, Sx, Sy |
are the full plastic moduli about the relevant axes |
| A |
is the gross cross‑sectional area |
| D, B and t |
are as defined in Section 3.3.2. |