6.1 Compression members: UB sections, UC sections and hollow sections
4.7.4 (a)
(a) Compression Resistance, Pc
(i) For non-slender (Class 1, 2 or 3) cross-sections:
Pc = Ag pc
where:
| Ag |
is the gross cross‑sectional area |
| pc |
is the compressive strength. |
4.7.5
Annex. C.2
Table 23
The compressive strength pc is obtained using the following values of Robertson constant, a.
| Type of Section |
Robertson constant a |
| Axis of buckling |
| x‑x |
y‑y |
| Hot-finished Structural Hollow sections |
2.0 |
2.0 |
| Cold-formed Structural Hollow sections |
5.5 |
5.5 |
| UB sections (flange thickness up to 40 mm) |
2.0 |
3.5 |
| UB sections (flange thickness over 40 mm) |
3.5 |
5.5 |
| UC sections (flange thickness up to 40 mm) |
3.5 |
5.5 |
| UC sections (flange thickness over 40 mm) |
5.5 |
8.0 |
| Joists (when D/B > 1.2) |
2.0 |
3.5 |
| Joists (when D/B ≤ 1.2) |
3.5 |
5.5 |
Note 1
For I and H sections with a flange thickness between 40 mm and 50 mm, the value of pc is taken as the average of the values obtained for thickness up to 40 mm and over 40 mm, as noted in Table 23.
(ii) For class 4 slender cross-sections:
| Pc = Aeff pcs |
for class 4 slender cross-sections |
4.7.4 (b)
where:
| Aeff |
is the effective cross-sectional area |
| pcs |
is the value of pc for a reduced slenderness = λ( Aeff / Ag)0.5 |
The section classification of a section is partly dependent on the level of axial load applied. None of the universal columns, joists or parallel flange channels can be slender under axial compression only, but some universal beams and hollow sections can be slender. Sections that can be slender under axial compression are marked thus *.
The sections concerned are:
Table 11 and Table 12
| UB, when |
d/t > 40ε |
| Hot-finished SHS, RHS, when |
d/t > 40ε |
| Cold-formed SHS, RHS, when |
d/t > 35ε |
| All CHS, when |
D/t > 80ε2 |
where:
| d |
is the depth of the web |
| t |
is the thickness of the web or wall |
| D |
outside diameter |
| ε |
= (275/py)0.5 |
| py |
is the design strength. |
If a cross-section can be slender under axial load, the tabulated compression resistance is only based on the slender cross-section equation (given above) if the value from this equation is greater than the axial load required to make the cross‑section slender. Otherwise, the compression resistance of a potentially slender section is given as the smaller of the non-slender compression resistance and the axial load required to make the section slender. Tabulated values based on the equation for slender cross-sections are printed in italic type.
An example is given below:
686 x 254 x 170 UB S275
For this section, d/t = 42.4 > 40ε
Hence, the section can become slender if axial load is sufficiently high.
The axial load at which the section becomes slender is 5410 kN.
This value is calculated by setting d/t for the section equal to the class 3 limit from BS 5950-1[1], Table 11 and then solving for the value of axial load (Fc).
| For LE = 4 m, |
Pcx = pcsAeff = 5660 kN |
(slender cross-section) |
Hence table shows 5660 kN in italic type because, pcs Aeff > value at which cross‑section becomes slender, 5410 kN.
| For LE = 12 m, |
Pcx = pcA = 5400 kN |
(non-slender cross-section) |
Hence the table shows 5400 kN in normal type because, pcA < value at which cross‑section becomes slender, 5410 kN.
(b) Compression resistances Pcx and Pcy
The values of compression resistance Pcx and Pcy for buckling about the two principal axes are based on:
4.7.3
- The effective lengths (LE) given at the head of the table.
- The slenderness (λ), calculated as follows:
For UB, UC, joist and hollow sections,
4.7.2
| λ = LE/rx |
for x axis buckling |
| λ = LE/ry |
for y axis buckling |
6.2 Compression members: Single parallel flange channels
(a) Compression Resistance, Pc = Ag pc
where:
| Ag |
is the gross cross-section area |
| pc |
is the compressive strength. |
Table 23
Annex C.2
Compressive strength Pc has been obtained using the Robertson constant, a, of 5.5. Note: None of the parallel flange channels are slender under axial compression
(b) The values of compression resistance Pcx and Pcy for buckling about the two principle axes have been based on:
- The effective lengths (LE) given at the head of the table.
- The slenderness (λ), calculated as follows:
(i) For a single channel subject to concentric axial load,
4.7.2
| λ = LE/rx |
for x axis buckling |
| λ = LE/ry |
for y axis buckling |
(ii) For a single channel connected only through its web,
- by two or more rows of bolts arranged symmetrically across the web or by equivalent welded connection, the slenderness, λ should be taken as the greater of:
4.7.10.4 (a)
Table 25
| λx = 0.85 Lx/rx |
and |
| λy = 1.0 Ly/ry |
but ≥ 0.7 Ly/ry + 30 |
- by two or more bolts arranged symmetrically in a single row across the web or by equivalent welded connection, the slenderness, λ should be taken as the greater of:
4.7.10.4 (b)
Table 25
| λx = 1.0 Lx/rx |
and |
| λy = 1.0 Ly/ry |
but ≥ 0.7 Ly/ry + 30 |
where:
| Lx and Ly |
are the lengths between intersections |
| rx and ry |
are the radii of gyration of the single channel about the x and y axes. |
6.3 Compound compression members: two parallel flange channels
This website does not contain resistance tables for two parallel flange channels, either laced or back to back.
6.4 Compression members: single angles
4.7.4
(a) Compression resistance, Pc = Ag pc
where:
Table 23
Annex C.2
| Ag |
is the gross cross-section area |
| pc |
is the compressive strength and has been obtained using a Robertson constant, a, of 5.5 |
In the case of a single bolt at each end, the compression resistance should be taken as 80% of that for an axially loaded member with the same slenderness. (Note: no values are given for this case).
3.6.5
Sections which are slender are marked * and their resistances have been calculated using a reduced design strength.
An angle cross-sections is slender if (using code notation):
Table 11
d/t or b/t > 15ε or (d + b) / t > 24ε
Or using the notation in these tables, the requirements become:
A/t or B/t > 15ε or (A + B) / t > 24ε
In these circumstances, the design strength is reduced by the least of these factors:
3.6.5
where:
(b) The values of compression resistance are based on:
- The length (L) between intersections of centroidal axes or setting out line of the bolts given at the head of the tables.
- The slenderness (λ), calculated as follows:
4.7.10.2 (a)
Table 25
(i) For two or more bolts in standard clearance holes in line along the angle at each end or an equivalent welded connection, the slenderness should be taken as the greater of:
| 0.85 Lv/rv |
but ≥ 0.7 Lv/rv + 15; |
and |
| 1.0 La/ra |
but ≥ 0.7 La/ra + 30; |
and |
| 0.85 Lb/rb |
but ≥ 0.7 Lb/rb + 30. |
4.7.10.2 (c)
Table 25
(iii) For a single bolt at each end, the 8 should be taken as the greater of:
| 1.0 Lv/rv |
but ≥ 0.7 Lv/rv + 15; |
and |
| 1.0 La/ra |
but ≥ 0.7 La/ra + 30; |
and |
| 1.0 Lb/rb |
but ≥ 0.7 Lb/rb + 30. |
where:
| rv |
is the minimum radius of gyration |
| ra |
is the radius of gyration about the axis parallel to the connected leg |
| rb |
is the radius of gyration about the axis perpendicular to the connected leg. |
6.5 Compound compression members: two angles
4.7.13
The tables assume that the angles are interconnected back to back, as recommended in Clause 4.7.13 of the code.
(a) Compression resistance, Pc = Ag pc
where:
Table 23
Annex C.2
| Ag |
is the gross cross-section area of the two angles |
| pc |
is the compressive strength and has been obtained using a Robertson constant of 5.5. |
3.6.5
Sections which are slender are marked * and their resistances have been calculated using a reduced design strength.
An angle cross-sections is slender if (using code notation):
Table 11
d/t or b/t > 15ε or (d + b)/t > 24ε
Or using the notation in these tables, the requirements become:
A/t or B/t > 15ε or (A + B)/t > 24ε
In these circumstances, the design strength is reduced by the least of these factors:
3.6.5
where:
(b) The values of compression resistance are based on:
- The length (L) between intersections of centroidal axes or setting out line of the bolts given at the head of the tables.
- The slenderness (λ), calculated as follows:
4.7.10.3 (a)
Table 25
(i) For double angles connected to one side of a gusset or member by two or more bolts in line along each angle, or by an equivalent weld at each end, the slenderness λ should be taken as the greater of:
| 1.0 Lx/rxm |
but ≥ 0.7 Lx/rxm + 30; |
and |
| [(0.85 Ly/rym)2 + λc2]0.5 |
but ≥ 1.4 λc |
4.7.10.3 (b)
Table 25
(ii) For double angles connected to one side of a gusset or member by one bolt in each angle, the slenderness λ should be taken as the greater of:
| 1.0 Lx/rxm |
but ≥ 0.7 Lx/rxm + 30; |
and |
| [(1.0 Ly/rym)2 + λc2]0.5 |
but ≥ 1.4 λc |
4.7.10.3 (c)
Table 25
(iii) For double angles connected to both sides of a gusset or member by two or more bolts in line along each angle, the slenderness λ should be taken as the greater of:
| 0.85 Lx/rxm |
but ≥ 0.7 Lx/rx + 30; |
and |
| [(1.0 Ly/rym)2 + λc2]0.5 |
but ≥ 1.4 λc |
4.7.10.3 (e)
Table 25
(iv) For double angles connected to both sides of a gusset or member by a single bolt in each angle, the slenderness λ should be taken as the greater of:
| 1.0 Lx/rxm |
but ≥ 0.7 Lx/rxm + 30; |
and |
| [(1.0 Ly/rym)2 + λc2]0.5 |
but ≥ 1.4 λc |
For double angles connected to both sides of a gusset or member by a single bolt in each angle, the compression resistance should be taken as 80% of that for an axially loaded member with the same slenderness. (Note: no values are given for this case).
Where:
| λc |
= Lc/rv but not greater than 50 |
| rv |
is the minimum radius of gyration of a single angle |
| rxm and rym are the radii of gyration of the double angles about the x and y axes |
4.7.9 (c)
| Lc |
is the length L divided by the number of bays. There are a sufficient number of bays so that λc ≤ 50. The number of bays is at least three and if there are more than three, the compression resistance is printed in bold type. |




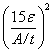 :
: 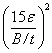 :
: 