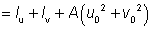6.1Compression members: UB and UC sections
6.2.4
6.2.4 (2)
(a) Design resistance of the cross section Nc,Rd
The design resistance is given by:
(i) For Class 1, 2 or 3 cross sections:
(ii) For Class 4 cross sections:
where:
| A |
is the gross area of the cross section |
| fy |
is the yield strength |
| Aeff |
is the effective area of the cross section in compression |
| γM0 |
is the partial factor for resistance of cross sections (γM0 = 1.0 as given in the National Annex) |
For Class 1, 2 and 3 cross sections the value of Nc,Rd is the same as the plastic resistance, Npl,Rd given in the tables for axial force and bending, and is therefore not given in the compression tables.
For Class 4 sections the value of Nc,Rd can be calculated using the effective areas tabulated in the tables of dimensions and gross section properties and the tables of effective section properties within this website. The values are not shown in the tables.
None of the universal columns are Class 4 under axial compression alone according to BS EN 1993-1-1, but some universal beams are Class 4 and these sections are marked thus *.
Table 5.2
The sections concerned are UB where the width to thickness ratio for the web in compression is:
c / t = d / tw > 42ε
where:
| d |
is the depth of straight portion of the web (i.e. the depth between fillets) |
| tw |
is the thickness of the web |
| ε |
= (235/fy)0.5 |
| fy |
is the yield strength. |
6.3.1.1
(b) Design buckling resistance
Design buckling resistances for two modes of buckling are given in the tables:
- Flexural buckling resistance, about each of the two principal axes: Nb,y,Rd and Nb,z,Rd
- Torsional buckling resistance, Nb,T,Rd
No resistances are given for torsional-flexural buckling because this mode of buckling does not occur in doubly symmetrical cross sections.
(i) Design flexural buckling resistance, Nb,y,Rd and Nb,z,Rd
The design flexural buckling resistances Nb,y,Rd and Nb,z,Rd depend on the non-dimensional slenderness (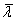 ), which in turn depends on:
), which in turn depends on:
- The buckling lengths (Lcr) given at the head of the table
- The properties of the cross section.
6.3.1.3
The non-dimensional slenderness has been calculated as follows:
For Class 1, 2 or 3 cross sections:
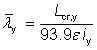 |
for y-y axis buckling |
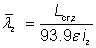 |
for z-z axis buckling |
For Class 4 cross sections:
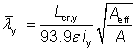 |
for y-y axis buckling |
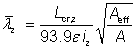 |
for z-z axis buckling |
where:
| Lcr,y, Lcr,z |
are the buckling lengths for the y-y and z-z axes respectively |
| iy, iz |
are the radii of gyration about y-y and z-z axes respectively. |
The tabulated buckling resistance is only based on Class 4 cross section properties if this value of force is sufficient to make the cross section Class 4 under combined axial force and bending. The value of n (= NEd/Npl,Rd) at which the cross section becomes Class 4 is shown in the tables for axial force and bending. Otherwise, the buckling resistance is based on Class 3 cross section properties. Tabulated values based on the Class 4 cross section properties are printed in italic type.
An example is given below:
533 x 210 x 101 UB S275
For this section, c/t = d/tw = 44.1 > 42ε = 39.6
Hence, the cross section is Class 4 under compression alone.
The value of axial force at which the section becomes Class 4 is NEd = 2890 kN (see axial force and bending table, where n = 0.845 and Npl,Rd = 3420 kN).
For Lcr,y = 4 m, Nb,y,Rd = 3270 kN
The table shows 3270 kN in italic type because the value is greater than the value at which the cross section becomes Class 4
For Lcr,y = 14 m, Nb,y,Rd = 2860 kN
The table shows 2860 kN in normal type because the value is less than the value at which cross–section becomes Class 4 (2890 kN).
(ii) Design torsional buckling resistance, Nb,T,Rd
6.3.1.4
The design torsional buckling resistance Nb,T,Rd depends on the non-dimensional slenderness (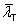 ), which in turn depends on:
), which in turn depends on:
- The buckling lengths (Lcr) given at the head of the table
- The properties of the cross section.
The non-dimensional slenderness has been calculated as follows:
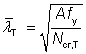 |
for Class 1, 2 or 3 cross sections |
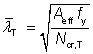 |
for Class 4 cross sections |
where:
| Ncr,T |
is the elastic torsional buckling force, given by 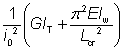 |
where:
|
i0
|
= 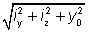 |
| y0 |
is the distance from the shear centre to the centroid of the gross cross section along the y-y axis (zero for doubly symmetric sections). |
6.2Compression members: hollow sections
6.2.4
6.2.4 (2)
(a) Design resistance of the cross section Nc,Rd
The design resistance is given by:
(i) For Class 1, 2 or 3 cross sections:
(ii) For Class 4 cross sections:
where:
| A |
is the gross area of the cross section |
| fy |
is the yield strength |
| Aeff |
is the effective area of the cross section in compression |
| γM0 |
is the partial factor for resistance of cross sections (γM0 = 1.0 as given in the National Annex). |
For Class 1, 2 and 3 cross sections, the value of Nc,Rd is the same as the plastic resistance, Npl,Rd given in the tables for axial force and bending, and is therefore not given in the compression tables.
For Class 4 sections, the value of Nc,Rd can be calculated using the effective areas tabulated in the tables of dimensions and gross section properties and the tables of effective section properties within this website of this website. The values are not shown in the tables.
Sections that are Class 4 under axial compression are marked thus *. The sections concerned are:
Table 5.2
- Square hollow sections, where c / t > 42ε and c = h – 3t
- Rectangular hollow sections, where cw / t > 42ε and cw = h – 3t
- Circular hollow sections, where d/t > 90ε2
where:
| h |
is the overall depth of the cross section |
| t |
is the thickness of the wall |
| ε |
= (235/fy)0.5 |
| fy |
is the yield strength. |
where De is defined in Section 4.2.
6.3.1.1
(b) Design buckling resistance
Design buckling resistances for flexural buckling are given in the tables.
The design flexural buckling resistances Nb,y,Rd and Nb,z,Rd depend on the non-dimensional slenderness (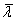 ), which in turn depends on:
), which in turn depends on:
- The buckling lengths (Lcr) given at the head of the table
- The properties of the cross section.
6.3.1.3
The non-dimensional slenderness has been calculated as follows:
For Class 1, 2 or 3 cross sections:
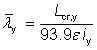 |
for y-y axis buckling |
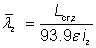 |
for z-z axis buckling |
For Class 4 cross sections:
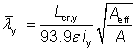 |
for y-y axis buckling |
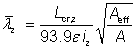 |
for z-z axis buckling |
where:
| Lcr,y, Lcr,z |
are the buckling lengths for the y-y and z-z axes respectively. |
| iy, iz |
are the radii of gyration about the y-y and z-z axes respectively. |
The tabulated buckling resistance is only based on Class 4 cross section properties when the value of the force is sufficient to make the cross section Class 4 under combined axial force and bending. The value of n ( = NEd / Npl,Rd) at which the cross section becomes Class 4 is shown in the tables for axial force and bending. Otherwise, the buckling resistance is based on Class 3 cross section properties. Tabulated values based on the Class 4 cross section properties are printed in italic type.
For Class 4 circular hollow sections, BS EN 1993-1-1 refers the user to BS EN 1993-1-6. Resistance values for these sections have not been calculated and the symbol $ is shown instead.
For Class 4 elliptical hollow sections, the design buckling resistance has been taken as the greater of:
- The design buckling resistance based on an effective area (see Section 4.2) and
- The design buckling resistance based on the gross area, but reducing the design strength such that the section remains Class 3. The reduced design strength fy,reduced is given by fy,reduced =
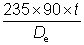
De is defined in Section 4.2.
6.3Compression members: parallel flange channels
6.2.4
6.2.4 (2)
(a) Design resistance of the cross section Nc,Rd
The design resistance is given by:
where:
| A |
is the gross area of the cross section |
| fy |
is the yield strength |
| γM0 |
is the partial factor for resistance of cross sections (γM0 = 1.0 as given in the National Annex). |
The value of Nc,Rd is the same as the plastic resistance, Npl,Rd given in the tables for axial force and bending, and is therefore not given in the compression tables.
6.3.1
(b) Design buckling resistance
Design buckling resistance values are given for the following cases:
- Single channel subject to concentric axial force
- Single channel connected only through its web, by two or more bolts arranged symmetrically in a single row across the web.
1. Single channel subject to concentric axial force
Design buckling resistances for two modes of buckling are given in the tables:
- Flexural buckling resistance about the two principal axes: Nb,y,Rd and Nb,z,Rd
- Torsional or torsional-flexural buckling resistance, whichever is less, Nb,T,Rd
(i) Design flexural buckling resistance, Nb,y,Rd and Nb,z,Rd
The design flexural buckling resistances Nb,y,Rd and Nb,z,Rd depend on the non-dimensional slenderness (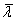 ) which in turn depends on:
) which in turn depends on:
- The buckling lengths (Lcr) given at the head of the table
- The properties of the cross section.
- The non-dimensional slenderness, which has been calculated as follows:
6.3.1.3
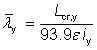 |
for y-y axis buckling |
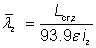 |
for z-z axis buckling |
where:
| Lcr,y, Lcr,z |
are the buckling lengths for the y-y and z-z axes respectively. |
6.3.1.4
(ii) Design torsional and torsional-flexural buckling resistance, Nb,T,Rd
The resistance tables give the lesser of the torsional and the torsional-flexural buckling resistances. These resistances depend on the non-dimensional slenderness (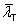 ), which in turn depends on:
), which in turn depends on:
- The buckling lengths (Lcr) given at the head of the table
- The properties of the cross section
- The non-dimensional slenderness, which has been calculated as follows:
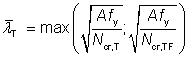
where:
| Ncr,T |
is the elastic torsional buckling force, = 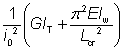 |
| i0 |
= 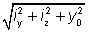 |
| y0 |
is the distance along the y- axis from the shear centre to the centroid of the gross cross section. |
| Ncr,TF |
is the elastic torsional‑flexural buckling force, = AσTF |
| σTF |
= 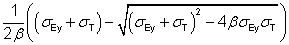 |
| σEy |
= 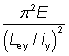 |
| σT |
= Ncr,T / A |
| b |
= 1 – (y0/i0)2 |
| Ley |
is the unrestrained length considering buckling about the y-y axis. |
2. Single channel connected only through its web, by two or more bolts arranged symmetrically in a single row across the web
Design buckling resistances for two modes of buckling are given in the tables:
6.3.1
- Flexural buckling resistance about each of the two principal axes: Nb,y,Rd and Nb,z,Rd
- Torsional or torsional-flexural buckling resistance, whichever is less, Nb,T,Rd
(i) Design flexural buckling resistance, Nb,y,Rd and Nb,z,Rd
The design flexural buckling resistances Nb,y,Rd and Nb,z,Rd depend on the non-dimensional slenderness (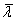 ), which in turn depends on:
), which in turn depends on:
- The system length (L) given at the head of the tables. L is the distance between intersections of the centroidal axes of the channel and the members to which it is connected.
- The properties of the cross section.
- The non-dimensional slenderness, which has been calculated as follows:
Annex BB.1.2
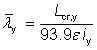 |
for y-y axis buckling |
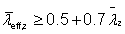 |
where |
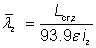 |
for z-z axis buckling |
(Based on a similar rationale given in Annex BB.1.2 for angles)
where:
| Lcr,y, Lcr,z |
are the lengths between intersections |
| iy, iz |
are the radii of gyration about the y-y and z-z axes. |
| ε |
= (235/fy)0.5. |
6.3.1.4
(ii) Design torsional and torsional-flexural buckling resistance, Nb,T,Rd
The torsional and torsional-flexural buckling resistance has been calculated as given above for single channels subject to concentric force.
6.4Compression members: single angles
6.3.1.1
(a) Design buckling resistance
Design buckling resistances for 2 modes of buckling, noted as F and T, are given in the tables:
- F: Flexural buckling resistance (taking torsional-flexural buckling effects into account), Nb,y,Rd and Nb,z,Rd
- T: Torsional buckling resistance, Nb,T,Rd.
(i) Design flexural buckling resistance, Nb,y,Rd, Nb,z,Rd
The tables give the lesser of the design flexural buckling resistance and the torsional flexural buckling resistance.
The design flexural buckling resistances Nb,y,Rd and Nb,z,Rd depend on the non-dimensional slenderness (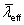 ), which in turn depends on:
), which in turn depends on:
- The system length (L) given at the head of the tables. L is the distance between intersections of the centroidal axes (or setting out line of the bolts) of the angle and the members to which it is connected.
- The properties of the cross section.
- The non-dimensional slenderness, which has been calculated as follows:
For two or more bolts in standard clearance holes in line along the angle at each end or an equivalent welded connection, the slenderness has been taken as:
EN 1993-1-1 BB.1.2(2)
For Class 3 cross sections:
For Class 4 cross sections:
where:
| Ly, Lz and Lv |
are the system lengths between intersections. |
These expressions take account of the torsional flexural buckling effects as well as the flexural buckling effects.
For the case of a single bolt at each end, BS EN 1993-1-1 refers the user to 6.2.9 to take account of the eccentricity. (Note: no values are given for this case).
6.3.1.3
(ii) Design torsional buckling resistance, Nb,T,Rd
The design torsional buckling resistance Nb,T,Rd depends on the non-dimensional slenderness (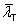 ), which in turn depends on:
), which in turn depends on:
- The system length (L) given at the head of the table
- The properties of the cross section
- The non-dimensional slenderness, which has been calculated as follows:
6.3.1.4(2)
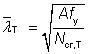 |
for Class 1, 2 or 3 cross sections |
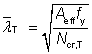 |
for Class 4 cross sections |
where:
| Ncr,T |
is the elastic torsional buckling force = 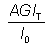 |
| G |
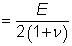 is the shear modulus is the shear modulus |
| E |
is the modulus of elasticity |
| ν |
is Poisson’s ratio (= 0.3) |
| IT |
is the torsional constant |
| I0 |
= 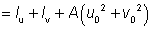 |
| Iu |
is the second moment of area about the u-u axis |
| Iv |
is the second moment of area about the v-v axis |
| u0 |
is the distance from shear centre to the v-v axis |
| v0 |
is the distance from shear centre to the u-u axis. |




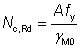
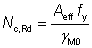
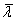 ), which in turn depends on:
), which in turn depends on: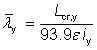
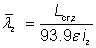
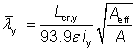
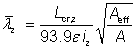
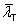 ), which in turn depends on:
), which in turn depends on: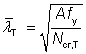
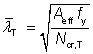
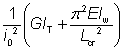
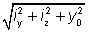
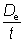 > 90ε2 (See
> 90ε2 (See 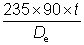
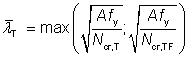
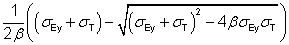
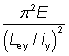
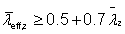
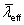 ), which in turn depends on:
), which in turn depends on: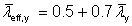
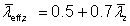
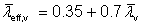
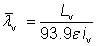
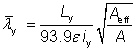
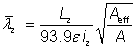
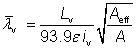
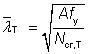
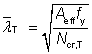
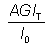
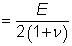 is the shear modulus
is the shear modulus